Difference between revisions of "Machine Learning"

Title: Automatic generation of domain ontologies
Description: This thesis to be developed together with Noustat S.r.l. (see http://www.noustat.it), who are developing research activities directed toward the optimization of knowledge management services, in collaboration with another company operating in this field. This project is aimed at removing the ontology building bottleneck, long and expensive activity that usually requires the direct collaboration of a domain expert. The possibility of automatic building the ontology, starting from a set of textual documents related to a specific domain, is expected to improve the ability to provide the knowledge management service, both by reducing the time-to-application, and by increasing the number of domains that can be covered. For this project, unsupervised learning methods will be applied in sequence, exploiting the topological properties of the ultra-metric spaces that emerge from the taxonomic structure of the concepts present in the texts, and associative methods will extend the concept network to lateral, non-hierarchical relationships.
Tutor: MatteoMatteucci, AndreaBonarini, DavideEynard
Additional Info: CFU 20 - 20 / Master of Science / Thesis

Title: Behavior recognition from visual data
Description: In the literature several approaches have been used to model observed behaviors and these date back to early approaches in animal behavior analysis (Baum and Eagon, 1967)(Colgan, 1978). Nowadays several techniques are used and they can be roughly classified as: State space models, Automata (e.g., Finite State Machines, Agents, etc.), Grammars (e.g., strings, T-Patterns, etc.), Bayeasian models (e.g., Hidden Markov Models), and Dynamic State Variables. The work will leverage on a huge corpus of techniques to devise the most suitable for behavior recognition from visual data. We exclude from the very beginning any deterministic approach being the phenomenon under observation complex and affected by noisy observations. The focus will be mainly of the use of dynamic graphical models (Ghahramani, 1998) and the application of bottom up learning techniques (Stolcke and Omohundro, 1993)(Stolcke and Omohundro, 1994) for model induction.

• L. E. Baum and J. A. Eagon. An inequality with applications to statistical estimation for probabilistic functions of markov processes and to a model for ecology. Bull. Amer. Math. Soc, 73(73):360–363, 1967.
• P. W. Colgan. Quantitative Ethology. John Wiley & Sons, New York, 1978.
• A. Stolcke and S. M. Omohundro. Hidden markov model induction by bayesian model merging. In Stephen Jos é Hanson, Jack D. Cowan, and C. Lee Giles, editors, Advances in Neural Information Processing Systems, volume 5. Morgan Kaufmann, San Mateo, CA, 1993.
• Zoubin Ghahramani. Learning dynamic bayesian networks. Lecture Notes in Computer Science, 1387:168, 1998.
• A. Stolcke and S. M. Omohundro. Best-first model merging for hidden markov model induction. Technical Report TR-94-003, 1947 Center Street, Berkeley, CA, 1994.

Material:

• papers from major journals and conferences
• kinet SDK for the extraction of body poses

Expected outcome:

• general framework for the recognition of behaviors from time series
• toolkit for behavior segmentation and recognition from time series
• running prototype based on data coming from the Microsoft kinect sensor

Required skills or skills to be acquired:

• understanding of techniques for behavior recognition
• background on pattern recognition and stochastic models
• basic understanding of computer vision
• C++ programming under Linux or Matlab
  

Tutor: MatteoMatteucci, AndreaBonarini
Additional Info: CFU 20 - 20 / Master of Science / Thesis

Title: Combinatorial optimization based on stochastic relaxation
Description: The project will focus on the study, implementation, comparison and analysis of different algorithms for the optimization of pseudo-Boolean functions, i.e., functions defined over binary variables with values in R. These functions have been studied a lot in the mathematical programming literature, and different algorithms have been proposed (1). More recently, the same problems have been faced in evolutionary computations, with the use of genetic algorithms, and in particular estimation of distribution algorithms (2,3). Estimation of distribution algorithms are a recent meta-heuristic, where classical crossover and mutation operators used in genetic algorithms are replaced with operators that come from statistics, such as sampling and estimation.

The focus will be on the implementation of a new algorithm able to combine different approaches (estimation and sampling, from one side, and exploitation of prior knowledge about the structure of problem, on the other), together with the comparison of the results with existing techniques that historically appear in different (and often separated) communities. Good coding (C/C++) abilities are required. Since the approach will be based on statistical models, the student is supposed to be comfortable with notions that come from probability and statistics courses. The project could require some extra effort in order to build and consolidate some background in math, especially in Bayesian statistics and MCMC techniques, such as Gibbs and Metropolis samplers (4).

The project can be extended to master thesis, according to interesting and novel directions of research that will emerge in the first part of the work. Possible ideas may concern the proposal of new algorithms able to learn existing dependencies among the variables in the function to be optimized, and exploit them in order to increase the probability to converge to the global optimum.

Picture taken from http://www.ra.cs.uni-tuebingen.de/

Bibliography

1. Boros, Endre and Boros, Endre and Hammer, Peter L. (2002) Pseudo-boolean optimization. Discrete Applied Mathematics.
2. Pelikan, Martin; Goldberg, David; Lobo, Fernando (1999), A Survey of Optimization by Building and Using Probabilistic Models, Illinois: Illinois Genetic Algorithms Laboratory (IlliGAL), University of Illinois at Urbana-Champaign.
3. Larrañga, Pedro; & Lozano, Jose A. (Eds.). Estimation of distribution algorithms: A new tool for evolutionary computation. Kluwer Academic Publishers, Boston, 2002.
4. Image Analysis, Random Fields Markov Chain Monte Carlo Methods
   

Tutor: MatteoMatteucci, LuigiMalago
Additional Info: CFU 5 - 20 / Master of Science / Course, Thesis

Title: Combining Estimation of Distribution Algorithms and other Evolutionary techniques for combinatorial optimization
Description: The project will focus on the study, implementation, comparison and analysis of different algorithms for combinatorial optimization using techniques and algorithms proposed in Evolutionary Computation. In particular we are interested in the study of Estimation of Distribution Algorithms (1,2,3,4), a recent meta-heuristic, often presented as an evolution of Genetic Algorithms, where classical crossover and mutation operators, used in genetic algorithms, are replaced with operators that come from statistics, such as sampling and estimation.

The focus will be on the implementation of new hybrid algorithms able to combine estimation of distribution algorithms with different approaches available in the evolutionary computation literature, such as genetic algorithms and evolutionary strategies, together with other local search techniques. Good coding (C/C++) abilities are required. Some background in combinatorial optimization form the "Fondamenti di Ricerca Operativa" is desirable. The project could require some effort in order to build and consolidate some background in MCMC techniques, such as Gibbs and Metropolis samplers (4). The project could be extended to master thesis, according to interesting and novel directions of research that will emerge in the first part of the work.

Computer vision provides a large number of optimization problems, such as new-view synthesis, image segmentation, panorama stitching and texture restoration, among the others, (6). One common approach in this context is based on the use of binary Markov Random Fields and on the formalization of the optimization problem as the minimum of an energy function expressed as a square-free polynomial, (5). We are interested in the proposal, comparison and evaluation of different Estimation of Distribution Algorithms for solving real world problems that appear in computer vision.

Pictures taken from http://www.genetic-programming.org and (6)

Bibliography

1. Pelikan, Martin; Goldberg, David; Lobo, Fernando (1999), A Survey of Optimization by Building and Using Probabilistic Models, Illinois: Illinois Genetic Algorithms Laboratory (IlliGAL), University of Illinois at Urbana-Champaign.
2. Larrañga, Pedro; & Lozano, Jose A. (Eds.). Estimation of distribution algorithms: A new tool for evolutionary computation. Kluwer Academic Publishers, Boston, 2002.
3. Lozano, J. A.; Larrañga, P.; Inza, I.; & Bengoetxea, E. (Eds.). Towards a new evolutionary computation. Advances in estimation of distribution algorithms. Springer, 2006.
4. Pelikan, Martin; Sastry, Kumara; & Cantu-Paz, Erick (Eds.). Scalable optimization via probabilistic modeling: From algorithms to applications. Springer, 2006.
5. Image Analysis, Random Fields Markov Chain Monte Carlo Methods
6. Carsten Rother, Vladimir Kolmogorov, Victor Lempitsky, Martin Szummer. Optimizing Binary MRFs via Extended Roof Duality, CVPR 2007
   

Tutor: MatteoMatteucci, LuigiMalago
Additional Info: CFU 5 - 10 / Master of Science / Course, Thesis

Title: Information geometry and machine learning
Description: In machine learning, we often introduce probabilistic models to handle uncertainty in the data, and most of the times due to the computational cost, we end up selecting (a priori, or even at run time) a subset of all possible statistical models for the variables that appear in the problem. From a geometrical point of view, we work with a subset (of points) of all possible statistical models, and the choice of the fittest model in out subset can be interpreted as a the point (distribution) minimizing some distance or divergence function w.r.t. the true distribution from which the observed data are sampled. From this perspective, for instance, estimation procedures can be considered as projections on the statistical model and other statistical properties of the model can be understood in geometrical terms. Information Geometry (1,2) can be described as the study of statistical properties of families of probability distributions, i.e., statistical models, by means of differential and Riemannian geometry.

Information Geometry has been recently applied in different fields, both to provide a geometrical interpretation of existing algorithms, and more recently, in some contexts, to propose new techniques to generalize or improve existing approaches. Once the student is familiar with the theory of Information Geometry, the aim of the project is to apply these notions to existing machine learning algorithms.

Possible ideas are the study of a particular model from the point of view of Information Geometry, for example as Hidden Markov Models, Dynamic Bayesian Networks, or Gaussian Processes, to understand if Information Geometry can give useful insights with such models. Other possible direction of research include the use of notions and ideas from Information Geometry, such as the mixed parametrization based on natural and expectation parameters (3) and/or families of divergence functions (2), in order to study model selection from a geometric perspective. For example by exploiting projections and other geometric quantities with "statistical meaning" in a statistical manifold in order to chose/build the model to use for inference purposes.

Since the project has a theoretical flavor, mathematical inclined students are encouraged to apply. The project requires some extra effort in order to build and consolidate some background in math, partially in differential geometry, and especially in probability and statistics.

Bibliography

1. Shun-ichi Amari, Hiroshi Nagaoka, Methods of Information Geometry, 2000
2. Shun-ichi Amari, Information geometry of its applications: Convex function and dually flat manifold, Emerging Trends in Visual Computing (Frank Nielsen, ed.), Lecture Notes in Computer Science, vol. 5416, Springer, 2009, pp. 75–102
3. Shun-ichi Amari, Information geometry on hierarchy of probability distributions, IEEE Transactions on Information Theory 47 (2001), no. 5, 1701–1711.
   

Tutor: MatteoMatteucci, LuigiMalago
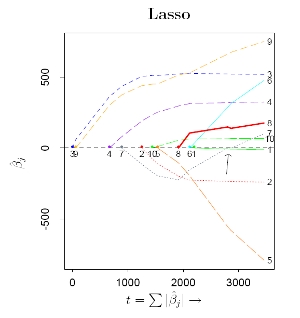
Additional Info: CFU 20 - 20 / Master of Science / Course, Thesis

Title: LARS and LASSO in non Euclidean Spaces
Description: LASSO (1) and more recently LARS (2) are two algorithms proposed for linear regression tasks. In particular LASSO solves a least-squares (quadratic) optimization problem with a constrain that limits the sum of the absolute value of the coefficients of the regression, while LARS can be considered as a generalization of LASSO, that provides a more computational efficient way to obtain the solution of the regression problem simultaneously for all values of the constraint introduced by LASSO.

One of the common hypothesis in regression analysis is that the noise introduced in order to model the linear relationship between regressors and dependent variable has a Gaussian distribution. A generalization of this hypothesis leads to a more general framework, where the geometry of the regression task is no more Euclidean. In this context different estimation criteria, such as maximum likelihood estimation and other canonical divergence functions do not coincide anymore. The target of the project is to compare the different solutions associated to different criteria, for example in terms of robustness, and propose generalization of LASSO and LARS in non Euclidean contexts.

The project will focus on the understanding of the problem and on the implementation of different algorithms, so (C/C++ or Matlab or R) coding will be required. Since the project has also a theoretical flavor, mathematical inclined students are encouraged to apply. The project may require some extra effort in order to build and consolidate some background in math, especially in probability and statistics.

Picture taken from (2)

Bibliography

1. Tibshirani, R. (1996), Regression shrinkage and selection via the lasso. J. Royal. Statist. Soc B., Vol. 58, No. 1, pages 267-288
2. Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani, Least Angle Regression, 2003
   

Tutor: MatteoMatteucci, LuigiMalago
Additional Info: CFU 20 - 20 / Master of Science / Course, Thesis

Title: Statistical inference for phylogenetic trees
Description: The project will focus on the study, implementation, comparison, and analysis of different statistical inference techniques for phylogenetic trees. Phylogenetic trees (1, 2, 3) are evolutionary trees used to represent the relationships between different species with a common ancestor. Typical inference tasks concern the construction of a tree starting from DNA sequences, involving both the choice of the topology of the tree (i.e., model selection) and the values of the parameters (i.e., model fitting). The focus will be a probabilistic description of the tree, given by the introduction of stochastic variables associated to both internal nodes and leaves of the tree.

The project will focus on the understanding of the problem and on the implementation of different algorithms, so (C/C++ or Matlab or R) coding will be required. Since the approach will be based on statistical models, the student is supposed to be comfortable with notions that come from probability and statistics courses.

The project is thought to be extended to master thesis, according to interesting and novel directions of research that will emerge in the first part of the work. Possible ideas may concern the proposal and implementation of new algorithms, based on recent approaches to phylogenetic inference available in the literature, as in (3) and (4). In this case the thesis requires some extra effort in order to build and consolidate some background in math in oder to understand some recent literature, especially in (mathematical) statistics and, for example, in the emerging field of algebraic statistics (5).

Other possible novel applications of phylogenetic trees have been proposed in contexts different from biology, as in (6). Malware (malicious software) is software designed to infiltrate a computer without the owner's informed consent. Often malwares are related to previous programs thought evolutionary relationships, i.e., new malwares appear as small mutations of previous softwares. We are interested in the use of techniques from phylogenetic trees to create a taxonomy of real world malwares.

Picture taken from http://www.tolweb.org/tree/ and http://www.blogscienze.com

Bibliography

1. Felsenstein 2003: Inferring Phylogenies
2. Semple and Steel 2003: Phylogenetics: The mathematics of phylogenetics
3. Louis J. Billera, Susan P. Holmes and and Karen Vogtmann Geometry of the space of phylogenetic trees. Advances in Applied Math 27, 733-767 (2001)
4. Evans, S.N. and Speed, T.P. (1993). Invariants of some probability models used in phylogenetic inference. Annals of Statistics 21, 355-377.
5. Lior Pachter, Bernd Sturmfels 2005, Algebraic Statistics for Computational Biology.
6. A. Walenstein, E-Md. Karim, A. Lakhotia, and L. Parida. Malware Phylogeny Generation Using Permutations of Code, Journal in Computer Virology, v1.1, 2005.
   

Tutor: MatteoMatteucci, LuigiMalago, StefanoZanero
Additional Info: CFU 5 - 20 / Master of Science / Course, Thesis