Difference between revisions of "Evoptool: Evolutionary Optimization Tool"
(→Graphic User Interface) |
(→Graphic User Interface) |
||
| Line 82: | Line 82: | ||
# ''Algorithms Panel.'' This panel allows to select a set of algorithms to compare in a particular execution. It is subdivided in four parts, in order to classify algorithms for belonging kind. Next, is possible to customize the parameters of each selected algorithm. | # ''Algorithms Panel.'' This panel allows to select a set of algorithms to compare in a particular execution. It is subdivided in four parts, in order to classify algorithms for belonging kind. Next, is possible to customize the parameters of each selected algorithm. | ||
# ''Result Tabs. ''This tabs show the result graphics of the a test execution in real time mode. At this time, only the average fitness graph is implemented in evoptool, but new graphs can be easily added in future. | # ''Result Tabs. ''This tabs show the result graphics of the a test execution in real time mode. At this time, only the average fitness graph is implemented in evoptool, but new graphs can be easily added in future. | ||
| − | # ''Log Monitor. '' | + | # ''Log Monitor. ''This monitor keep the user informed about the a test execution status and several others information. |
=== '''Command Line'''=== | === '''Command Line'''=== | ||
Revision as of 22:44, 27 May 2009
Project profile
| Name: | evoptool: Evolutive Optimization Tool. |
| Field: | Combining Estimation of Distribution Algorithms and other Evolutionary techniques
for combinatorial optimization. |
| Project's head: | M. Matteucci - User:MatteoMatteucci
L. Malagò - User:LuigiMalago |
| People involved: | G. Valentini - User:GabrieleValentini |
Short Description
The project focus on the study, implementation, comparison and analysis of different algorithms for combinatorial optimization using techniques and algorithms proposed in Evolutionary Computation. In particular we are interested in the study of Estimation of Distribution Algorithms, a recent meta-heuristic, often presented as an evolution of Genetic Algorithms, where classical crossover and mutation operators, used in genetic algorithms, are replaced with operators that come from statistics, such as sampling and estimation. The focus will be on the implementation of new hybrid algorithms able to combine estimation of distribution algorithms with different approaches available in the evolutionary computation literature, such as genetic algorithms and evolutionary strategies, together with other local search techniques.
User Manual
Algorthms
This section have the purpose to show the set of algorithms implemented inside evoptool. These algorithms belong to different classes, and they perfom different operations. In the following lines are presented the theoretical bases for better undestand the use of evoptool.
- Genetic Algorithm (GA). Is a search technique used in computing to find exact or approximate solutions to optimization and search problems. They grow a population of abstract representations (chromosomes or genotype) of candidate solutions (individuals or phenotypes) to an optimization problem evolves toward better solutions. In this tool, solutions are represented as binary strings of 0s and 1s, but other encodings are also possible. The evolution usually starts from a population of randomly generated individuals and happens in several generations (selection, crossover, mutation). The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. Nowaday, there are the following GA implemented inside evoptool:
- SGA (Simple Genetic Algorithm). A selection operator is applied to the population and two random recombinator operators called crossover and mutation are applied to the selected population in order to improve the population. SGA uses a truncation selection with a fixed percentage. The variation operators used are Uniform crossover and Bit-Flip mutation.
- SGA with Binary Tournment.
- SGA with Population Wise Uniform Crossover.
- SGA (Simple Genetic Algorithm). A selection operator is applied to the population and two random recombinator operators called crossover and mutation are applied to the selected population in order to improve the population. SGA uses a truncation selection with a fixed percentage. The variation operators used are Uniform crossover and Bit-Flip mutation.
- Estimation Distribution Algorithm (EDA). Is powerful population-based searcher where the variation operations traditionally implemented via crossover and mutation in EAs are replaced by the process of random sampling from a probability distribution. The distribution is modified generation after generation, using information obtained from the fitter individuals in the population (estimation). The objective of these changes in the distribution is to increase the probability of generating individuals with high fitness. In our tool there are several EDA implemented such:
- cGA (Compact Genetic Algorithm). It initialize a vector of probabilities where each component follows a Bernoulli distribution with parameter 0.5. Next, two individuals are generated randomly from this vector of probabilities. After the individuals are evaluated, a competion between then is carried out. The competion is held at level of each of the unidimensional variables, in such a way that if for the ith position the conquiring individual take a value different from the loser, the ith component of the vector of probabilities increases its value.
- PBIL (Population Based Incremental Learning). It maintains unconditional probabilities and no interparameter dependencies are modeled. A vector, P, specifies the probability of generating a 1 in each bit position. Initially, all values in P are set to 0.5. A number of solution vectors are generated by stochastically sampling P; each bitis sampled independently of all the others. The probability vector is then moved towards the generated solution vector with the highest evaluation.
- UMDA (Univariate Marginal Distribution Algorithm). At each generation, it estimate the joint probability distribution model of the selected individual by factorize it as product of indipendent univariate marginal distributions. Each univariate marginal distribution is estimated from marginal frequency.
- MIMIC (Mutual Information Maximizing Input Clustering). It attempts to communicate information about the cost function obtained from one iteration of the search to later iterations of the search directly. There are two main components of MIMIC: first, a randomized optimization algorithm that samples from those regions of the input space most likely to contain the maximum; second, an effective density estimator that can be used to capture a wide variety of structure on the input space, and that build a Markov Chain in order to represents the bivariate structure.
- COMIT (Combining Optimizers with Mutual Information Trees). It gains most of the benefits of modeling the dependencies in the search space at a significantly reduced computational cost. COMIT starts by estimating a probabilistic model of the population, than uses the model to stochastically generate new solutions, it selects the fittest solutions and perfom a local fast-search initialized with these solutions.
- COMIT with HillClimbing as fast-search.
- COMIT with PBIL as fast-search.
- DEUM (Distribution Estimation Using Markov Random Field). DEUM uses MRF approach to estimate and sample the probability distribution using a fitness modelling approach to estimate the MRF parameters. This version of DEUM is an univariate model of probability distribution. This allows to completely eliminate the structure learning task.
- DEUM with probability vector. It uses the estimated parameters of MRF for update the probability vector, generation by generation.
- DEUM with direct sampling from Gibbs distribution. It uses the estimated parameters of MFR for directly calcutate the probability of each bit to be 1 or 0.
- Is-DEUM (Ising model DEUM). It is an evolution from the univariate DEUM to a bivariate version. This algorithm has been defined for solve the Ising Sping Glass problem, and therefore it use a grid structure to model the interactions between each variables of a solution.
- Is-DEUM with a Metropolis sampler.
- Is-DEUM with a Gibbs sampler.
- sBOA (Simple Bayesian Optimization Algorithm). It is a multivariate EDA that uses the Bayesian Dirichlet equivalence metric to measure the goodness of each structure. The search used is a greedy search and it starts in each generation from scratch. In order to reduce the cardinality of the search space the constraint that each node in the Bayesian network as at most k parents is assumed.
- Genetic Estimation Distribution Algorithm (GEDA). This class of Evolute Algorithms is a new proposal class, where genetic variation operations such mutation and crossover are applied to a probabilistic model of the population, rather than directly to an individual of the population. Each generation of a GEDA is composed by estimation of population distribution, variation of the probabilistic model, and sampling from the variated model.
- gcGA.
- Operative Reaserch classical algorithms (OR). It is distinguished by its frequent use to examine an entire management information system, rather than concentrating only on specific elements. An operations researcher faced with a new problem is expected to determine which techniques are most appropriate given the nature of the system, the goals for improvement, and constraints on time and computing power. For this and other reasons, the human element of OR is vital. Like any other tools, OR techniques cannot solve problems by themselves.
- Pseudo Boolean Linear Programming.
Optimization Problems
An optimization problem is defined by a specified problem space X, an objective functions F , a search space G, a set of search operations A. Specifying the elements of this tuple is the most important prerequisite for any experiment. The problem space X is the space of all possible solutions canditates, in our case is defined by every combinations of a fixed lengh bit string. The objective functions F (fitness) measure the utility of a solution. As convention, we decide that every objective function return a real number between in the [0,100] set, and if nothing else is stated, maximization is assumed. The search space G is the space of elements where the search operations are applied. For evoptool is defined by the individual lenght (size). The search operations A are all the operations used for perform the search, and such we compare several algorthms a time, they are defined by the particular algorthm used.
Inside evoptool, is possible to choose between several different Objective Functions and customize a proper Optimization Problem setting the individual size and choosing a set of Algorithms to compare. The following list contains the Objective Functions implemented for the moment.
- AltBits.
- One Max and One Zero Max. The task in the OneMax problem is to find a binary string of length n consisting of all ones. The search and problem space are both the fixed-length bit strings G = X = Bn. Each gene (bit) has two alleles 0 and 1 which also contribute exactly this value to the total fitness.
- BinVal. It is something like a perverted version of the OneMax problem, with the objective function defined as the real value of the binary string. Since the bit at index i has a higher contribution to the fitness than all other bit at higher indices together, the comparison between two solution candidates x1 and x2 is won by the
lexicographically bigger one. We can expect that the bits with high contribution (high salience) will converge quickly whereas the other genes with lower salience are only pressured by selection when all others have already been fully converged.
- F3d Deceptive.
- F3d Deceptive Bipolar.
- F3d Deceptive Ovelapping.
- Four and Six Peaks. This Objective Function have some global optima wich are isolated, and therefore are difficult to find. It also have some local optima which are easy to get and therefore the search algorithms tend to converge on local optima.
- Trap5. Subjected to maximization based on the Hamming distance to a pre-defined global optimum X' . They build a second, local optimum in form of a hill with a gradient pointing away from the global optimum. This trap is specified with two values, b and r, where b corresponds to the width of the attractive basins (in our case b = 5)and r to their relative importance.
- Quadratic.
- Sat Lib.
- SumVal.
- Royal Road.
- Liepins Vose Fully Deceptive.
Graphic User Interface
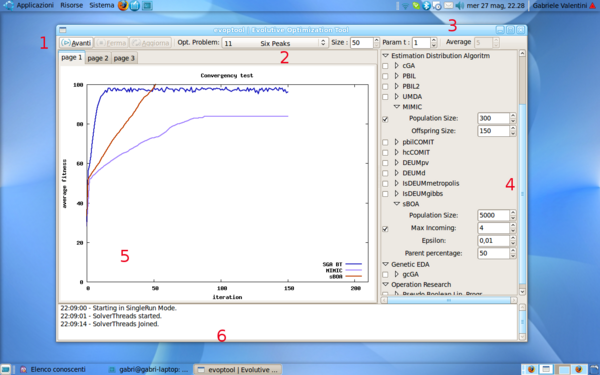
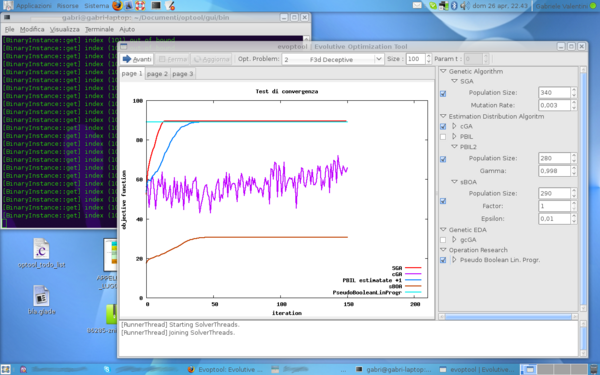
The graphic user interface of evoptool is quite intuitive. The user can easily customize his own experiment, and visualize the results graph. In the next rows there are shortly described the GUI componets and their use.
- Control Buttons. There are three control buttons which can be used to start or stop the execution of an experitment, and to force the update of the graphs.
- Objective Function Settings. This part of the toolbar allows the customization of the Objective Problem. It is possible to select an objective function type and fix the individual size as number of bits.
- Average Mode Setting. Pushing this toggled button it is possible to enable Average Test Mode. In this mode, evoptool will run a difined number of algortihms for each selected one in the Algorithm Panel, and it will perform the average of the different executions of the same algorithm. This option is usefull to show the average behavior of searchers.
- Algorithms Panel. This panel allows to select a set of algorithms to compare in a particular execution. It is subdivided in four parts, in order to classify algorithms for belonging kind. Next, is possible to customize the parameters of each selected algorithm.
- Result Tabs. This tabs show the result graphics of the a test execution in real time mode. At this time, only the average fitness graph is implemented in evoptool, but new graphs can be easily added in future.
- Log Monitor. This monitor keep the user informed about the a test execution status and several others information.
Command Line
Documentation
Evoptool is a software with the purpose to compare the performance of several different algorithms from the Evolutive family and, for obvious reasons, with some algorithms from the classical Operation Research family. Evoptool is written in C++ for the GNU/Linux platform and it exploit the Gtk libraries (in this case gtkmm libraries) and GNUplot utility. Inside this tool there are several implemented algorithms and some wrapped ones from already existing applications.
Software Modules
Evoptool is made up of several different modules (or libraries). This architecture make easy to organize files and better understanding how the application work.
- common - It contains commons classes and ancestors for the algorithm modules and for the optimization function module.
- ga - It contains the implementation of several Genetic Algorithms.
- eda - It contains the implementation of several Estimation Distribution Algorithms.
- geda - It contains the implementation of several gEDAs.
- or - It contains the implementation of some algorithms from the classical Operation Research.
- opt-pbl - It contains the implementation of several objective functions (fitness), that represents different problem instances.
- gui - This module is the main one, it contains all the classes for manage GUI (algorithm decorators). From the other side it implements the multithread mechanism under the GUI, and last but not list it contains the wrapped applications and take care about wrapping.
- misc - It contains general utility classes such rondom seed geerator.
- shared -
Hierarchies
Algorithms Hierarchy
Decorators Hierarchy
Objective Functions Hierarchy
Usefull Links
- Evoptool Repository (Need authentication!)
- GNU Scientific Library
- GUI Library Gtkmm
- Boost Library
- Gnuplot Utility
- C++ Library reference