Difference between revisions of "Evoptool: Evolutionary Optimization Tool"
(→Algorthms) |
(→Algorthms) |
||
| Line 44: | Line 44: | ||
*** ''Is-DEUM with a Metropolis sampler.'' | *** ''Is-DEUM with a Metropolis sampler.'' | ||
*** ''Is-DEUM with a Gibbs sampler.'' | *** ''Is-DEUM with a Gibbs sampler.'' | ||
| − | ** ''sBOA.'' | + | ** ''sBOA (Simple Bayesian Optimization Algorithm). ''It is a multivariate EDA that uses the Bayesian Dirichlet equivalence metric to measure the goodness of each structure. The search used is a greedy search and it starts in each generation from scratch. In order to reduce the cardinality of the search space the constraint that each node in the Bayesian network as at most ''k'' parents is assumed. |
* '''''Genetic Estimation Distribution Algorithm (GEDA). ''''' | * '''''Genetic Estimation Distribution Algorithm (GEDA). ''''' | ||
Revision as of 19:56, 27 May 2009
Project profile
| Name: | evoptool: Evolutive Optimization Tool. |
| Field: | Combining Estimation of Distribution Algorithms and other Evolutionary techniques
for combinatorial optimization. |
| Project's head: | M. Matteucci - User:MatteoMatteucci
L. Malagò - User:LuigiMalago |
| People involved: | G. Valentini - User:GabrieleValentini |
Short Description
The project focus on the study, implementation, comparison and analysis of different algorithms for combinatorial optimization using techniques and algorithms proposed in Evolutionary Computation. In particular we are interested in the study of Estimation of Distribution Algorithms, a recent meta-heuristic, often presented as an evolution of Genetic Algorithms, where classical crossover and mutation operators, used in genetic algorithms, are replaced with operators that come from statistics, such as sampling and estimation. The focus will be on the implementation of new hybrid algorithms able to combine estimation of distribution algorithms with different approaches available in the evolutionary computation literature, such as genetic algorithms and evolutionary strategies, together with other local search techniques.
User Manual
Algorthms
In this tool there are several bla bla bla..
- Genetic Algorithm (GA). Is a search technique used in computing to find exact or approximate solutions to optimization and search problems. They grow a population of abstract representations (chromosomes or genotype) of candidate solutions (individuals or phenotypes) to an optimization problem evolves toward better solutions. In this tool, solutions are represented as binary strings of 0s and 1s, but other encodings are also possible. The evolution usually starts from a population of randomly generated individuals and happens in several generations (selection, crossover, mutation). The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. Nowaday, there are the following GA implemented inside evoptool:
- SGA.
- SGA with Binary Tournment.
- SGA with Population Wise Uniform Crossover.
- SGA.
- Estimation Distribution Algorithm (EDA). Is powerful population-based searcher where the variation operations traditionally implemented via crossover and mutation in EAs are replaced by the process of random sampling from a probability distribution. The distribution is modified generation after generation, using information obtained from the fitter individuals in the population (estimation). The objective of these changes in the distribution is to increase the probability of generating individuals with high fitness. In our tool there are several EDA implemented such:
- cGA (Compact Genetic Algorithm). It initialize a vector of probabilities where each component follows a Bernoulli distribution with parameter 0.5. Next, two individuals are generated randomly from this vector of probabilities. After the individuals are evaluated, a competion between then is carried out. The competion is held at level of each of the unidimensional variables, in such a way that if for the ith position the conquiring individual take a value different from the loser, the ith component of the vector of probabilities increases its value.
- PBIL (Population Based Incremental Learning). It maintains unconditional probabilities and no interparameter dependencies are modeled. A vector, P, specifies the probability of generating a 1 in each bit position. Initially, all values in P are set to 0.5. A number of solution vectors are generated by stochastically sampling P; each bitis sampled independently of all the others. The probability vector is then moved towards the generated solution vector with the highest evaluation.
- UMDA (Univariate Marginal Distribution Algorithm). At each generation, it estimate the joint probability distribution model of the selected individual by factorize it as product of indipendent univariate marginal distributions. Each univariate marginal distribution is estimated from marginal frequency.
- MIMIC (Mutual Information Maximizing Input Clustering). It attempts to communicate information about the cost function obtained from one iteration of the search to later iterations of the search directly. There are two main components of MIMIC: first, a randomized optimization algorithm that samples from those regions of the input space most likely to contain the maximum; second, an effective density estimator that can be used to capture a wide variety of structure on the input space, and that build a Markov Chain in order to represents the bivariate structure.
- COMIT (Combining Optimizers with Mutual Information Trees). It gains most of the benefits of modeling the dependencies in the search space at a significantly reduced computational cost. COMIT starts by estimating a probabilistic model of the population, than uses the model to stochastically generate new solutions, it selects the fittest solutions and perfom a local fast-search initialized with these solutions.
- COMIT with HillClimbing as fast-search.
- COMIT with PBIL as fast-search.
- DEUM (Distribution Estimation Using Markov Random Field). DEUM uses MRF approach to estimate and sample the probability distribution using a fitness modelling approach to estimate the MRF parameters. This version of DEUM is an univariate model of probability distribution. This allows to completely eliminate the structure learning task.
- DEUM with probability vector. It uses the estimated parameters of MRF for update the probability vector, generation by generation.
- DEUM with direct sampling from Gibbs distribution. It uses the estimated parameters of MFR for directly calcutate the probability of each bit to be 1 or 0.
- Is-DEUM.
- Is-DEUM with a Metropolis sampler.
- Is-DEUM with a Gibbs sampler.
- sBOA (Simple Bayesian Optimization Algorithm). It is a multivariate EDA that uses the Bayesian Dirichlet equivalence metric to measure the goodness of each structure. The search used is a greedy search and it starts in each generation from scratch. In order to reduce the cardinality of the search space the constraint that each node in the Bayesian network as at most k parents is assumed.
- Genetic Estimation Distribution Algorithm (GEDA).
- gcGA.
- Operative Reaserch classical algorithms (OR).
- Pseudo Boolean Linear Programming.
Optimization Problems
An optimization problem is defined by a specified problem space X, an objective functions F , a search space G, a set of search operations A. Specifying the elements of this tuple is the most important prerequisite for any experiment. The problem space X is the space of all possible solutions canditates, in our case is defined by every combinations of a fixed lengh bit string. The objective functions F (fitness) measure the utility of a solution. As convention, we decide that every objective function return a real number between in the [0,100] set, and if nothing else is stated, maximization is assumed. The search space G is the space of elements where the search operations are applied. For evoptool is defined by the individual lenght (size). The search operations A are all the operations used for perform the search, and such we compare several algorthms a time, they are defined by the particular algorthm used.
Inside evoptool, is possible to choose between several different Objective Functions and customize a proper Optimization Problem setting the individual size and choosing a set of Algorithms to compare. The following list contains the Objective Functions implemented for the moment.
- AltBits.
- One Max and One Zero Max. The task in the OneMax problem is to find a binary string of length n consisting of all ones. The search and problem space are both the fixed-length bit strings G = X = Bn. Each gene (bit) has two alleles 0 and 1 which also contribute exactly this value to the total fitness.
- BinVal. It is something like a perverted version of the OneMax problem, with the objective function defined as the real value of the binary string. Since the bit at index i has a higher contribution to the fitness than all other bit at higher indices together, the comparison between two solution candidates x1 and x2 is won by the
lexicographically bigger one. We can expect that the bits with high contribution (high salience) will converge quickly whereas the other genes with lower salience are only pressured by selection when all others have already been fully converged.
- F3d Deceptive.
- F3d Deceptive Bipolar.
- F3d Deceptive Ovelapping.
- Four and Six Peaks.
- Trap5. Subjected to maximization based on the Hamming distance to a pre-defined global optimum X' . They build a second, local optimum in form of a hill with a gradient pointing away from the global optimum. This trap is specified with two values, b and r, where b corresponds to the width of the attractive basins (in our case b = 5)and r to their relative importance.
- Quadratic.
- Sat Lib.
- SumVal.
- Royal Road.
- Liepins Vose Fully Deceptive.
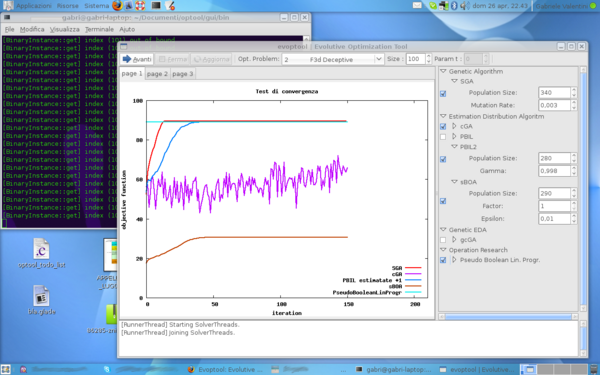
Graphic User Interface
Command Line
Documentation
Evoptool is a software with the purpose to compare the performance of several different algorithms from the Evolutive family and, for obvious reasons, with some algorithms from the classical Operation Research family. Evoptool is written in C++ for the GNU/Linux platform and it exploit the Gtk libraries (in this case gtkmm libraries) and GNUplot utility. Inside this tool there are several implemented algorithms and some wrapped ones from already existing applications.
Software Modules
Evoptool is made up of several different modules (or libraries). This architecture make easy to organize files and better understanding how the application work.
- common - It contains commons classes and ancestors for the algorithm modules and for the optimization function module.
- ga - It contains the implementation of several Genetic Algorithms.
- eda - It contains the implementation of several Estimation Distribution Algorithms.
- geda - It contains the implementation of several gEDAs.
- or - It contains the implementation of some algorithms from the classical Operation Research.
- opt-pbl - It contains the implementation of several objective functions (fitness), that represents different problem instances.
- gui - This module is the main one, it contains all the classes for manage GUI (algorithm decorators). From the other side it implements the multithread mechanism under the GUI, and last but not list it contains the wrapped applications and take care about wrapping.
- misc - It contains general utility classes such rondom seed geerator.
- shared -
Hierarchies
Algorithms Hierarchy
Decorators Hierarchy
Objective Functions Hierarchy
Usefull Links
- Evoptool Repository (Need authentication!)
- GNU Scientific Library
- GUI Library Gtkmm
- Boost Library
- Gnuplot Utility
- C++ Library reference