Wikipedia Category Graph
Automatically assigning Wikipedia articles to macrocategories
| |
| Short Description: | Represent Wikipedia Categories with a model based on graphs to further analyze it. |
| Coordinator: | MarcoColombetti (colombet@elet.polimi.it) |
| Tutor: | DavidLaniado (david.laniado@gmail.com), RiccardoTasso (tasso@elet.polimi.it) |
| Collaborator: | |
| Students: | JacopoFarina (jacopo1.farina@mail.polimi.it) |
| Research Area: | Social Software and Semantic Web |
| Research Topic: | Graph Mining and Analysis, Semantic Tagging |
| Start: | 2010/06/10 |
| End: | 2010/10/01 |
| Status: | Closed |
| Level: | Bs |
| Type: | Thesis |
The goal of the project is to analyze Wikipedia categories by representing them in a graph based database to further extract informations mainly about macrocategories.
Wikipedia categories are not a tree-based structure: a category may be contained in another one which is contained in another one which is contained in the first, generating a cyclic reference and many categories may be a root category (non contained in others).
For thess reasons a graph database is better to represent the structure.
Contents
Creation and further analysis of the database with igraph
Wikipedia lets users download the entire site database (with all versions of all articles) or just some selections of it. We use a selection which contains the category structure and article memberships in them.
Neo4j is a graph-based database, which allow a program to create and manipulate graph structures like nodes and relationships.
In order to transfer the database in neo4j format is better save it in a file, which will be read one line at time.
After transferring the structure in a Neo4j graph it is possible to create from it a Pajek file (.net) to make general analysis like described here.
Results of the analysis
We can use the tools described here
The diameter of the graph is 32. This is the maximum distance (number of nodes in the minimum path) between two nodes. These two nodes are Prehistoric life sorted by geography (A category about prehistoric animals without articles) and BMW M20 (a car).
The average distance between two nodes is 5.5568.
The graph density is 6.28*10-7. This is the ratio of the number of edges and the number of possible edges.
By analysing the graph with little Java programs written for this task we calculated the average number of categories per article is 2.68.
Statistically, the 93% of articles has less than 7 categories, 64% less than 3.
The article with more categories is Winston Churchill, with 70 categories. Albert Einstein has the notable number of 56 categories, too.
Strongly connected components
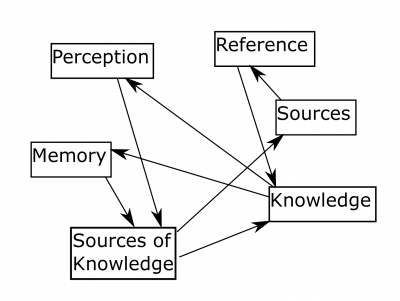
By applying the Tarjan's strongly connected components algorithm to the graph is possible to found 93 structures of up to 2 nodes. Each of them contains at least one cycle. Most of them are composed of two categories about the same thing, like History of the Germanic peoples and Ancient Germanic peoples, but there are also more curious cases like this one
Tested algorithms
We tried 9 algorithms to choose the category which fit best an article. After confronting the results of the automatic procedure with human made assignments, the best algorithm was choose a different weight to each edge by the traversal direction.
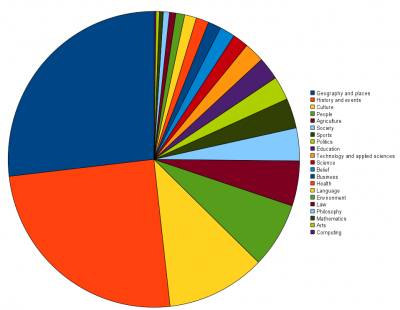
Sizes of the macrocategories determined this way are:
Download
- The relation about the project (in Italian) can be found here
- Sources in Java can be found here
- Slides of the thesis (in Italian) here
- The thesis (in Italian) here