Difference between revisions of "PIXYBOT"
From AIRWiki
DavideLaudi (Talk | contribs) (Created page with "{{Project |title=Loop-closure detection in mobile robotics |image= |short_descr= |coordinator=MatteoMatteucci |tutor=MatteoMatteucci |collaborator= |students=DavideLaudi |resarea...") |
|||
| Line 1: | Line 1: | ||
{{Project | {{Project | ||
| − | |title= | + | |title=EKF on Manifolds |
| − | |image= | + | |image=SE3_Manifold.jpg |
| − | |short_descr= | + | |short_descr=Extended Kalman Filtering operating on Lie Groups |
|coordinator=MatteoMatteucci | |coordinator=MatteoMatteucci | ||
| − | |tutor= | + | |tutor=DavideCucci |
| − | |collaborator= | + | |collaborator=None |
| − | |students= | + | |students=SimoneStefanini |
|resarea=Robotics | |resarea=Robotics | ||
| − | |restopic= | + | |restopic=None |
| − | |start= | + | |start=01/05/2013 |
|end= | |end= | ||
|status=Active | |status=Active | ||
}} | }} | ||
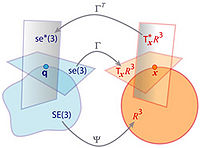
| − | The aim | + | Extended Kalman filtering is a well known technique for the estimation of the state of a dynamical system also used in robotics for localization and mapping. However in the basic formulation it assumes all variables to live in an Euclidean space while some components may span over the non-Euclidean 2D or 3D rotation group SO(2) or SO(3). The aim of this project is to write an Extended Kalman filter to operate on Lie Groups to take into account the presence of manifolds. |
Revision as of 06:57, 3 May 2013
EKF on Manifolds
| |
| Short Description: | Extended Kalman Filtering operating on Lie Groups |
| Coordinator: | MatteoMatteucci (matteo.matteucci@polimi.it) |
| Tutor: | DavideCucci (cucci@elet.polimi.it) |
| Collaborator: | None () |
| Students: | SimoneStefanini (simone.stefanini@mail.polimi.it) |
| Research Area: | Robotics |
| Research Topic: | None |
| Start: | 01/05/2013 |
| Status: | Active |
Extended Kalman filtering is a well known technique for the estimation of the state of a dynamical system also used in robotics for localization and mapping. However in the basic formulation it assumes all variables to live in an Euclidean space while some components may span over the non-Euclidean 2D or 3D rotation group SO(2) or SO(3). The aim of this project is to write an Extended Kalman filter to operate on Lie Groups to take into account the presence of manifolds.